地震の震源域で生じた現象そのものの大きさを表す尺度がマグニチュード(M)です． 日本語では「規模」と称される場合もあります． 規模の大きな地震でも遠く離れていれば地面の揺れは小さいし，逆に小規模の地震でもごく近傍で発生すれば大きな揺れが記録されます． このため，地震の規模の大小を公平に判断するためには，震源から同じ距離だけ離れた地点において揺れ具合を比較せねばなりません．

　マグニチュードは，このような趣旨で，米国カリフォルニア州に発生する地震の規模を客観的に評価する尺度として，1935年，リヒター(Richter)によって導入されました． すなわち，震源から100km離れた地点に置かれた当時の標準地震計(ウッド・アンダーソン型地震計)で記録された揺れの最大振幅をミクロン(μm)単位で表わし，その数値の対数をマグニチュード(M)として定義しました．
　このため，欧米では，マグニチュードよりも「リヒター・スケール」という用語がよく使われます． 現実には，震源からちょうど100kmの地点に都合よく地震計が設置されているとは限らず，また地震計にも様々なタイプのものがあるため，当初定義されたマグニチュードに準拠する形で種々の補正式が考案され，各国で使用されるようになっています．

　なお，2.2節で示すように，大きな地震になるほど，そこから放出される地震波の卓越周期（もっとも優勢な揺れ方の周期）は長くなる性質があります． 一方，9.1節で示すように，地震計は自分自身の固有周期（振子を自然に１回振らせたときの所要時間）よりも ゆっくりとした地面の揺れに対しては感度が鈍るという特性をもっているため，個々の地震計は，その周波数特性の限界によって， 長周期の地震波を十分に記録できず，大きな地震に対するマグニチュードを正確に見積もれなくなります．
　このため，短周期地震計を用いて見積もる「実体波マグニチュード」(m_B：周期数秒の地震波を用いる)や，長周期地震計を用いて見積もる「表面波マグニチュード」(Ms：周期20〜30秒の地震波を用いる)は，巨大な地震に対して “マグニチュードの頭打ち” という問題が生じます．
　最近では，このような飽和の心配がない「モーメント・マグニチュード」(Mw)が使用されるようになってきました． 「モーメント・マグニチュード」は，震源で生じた断層運動の強さに基づいて定義されており，断層面の面積と岩盤の食い違い量との積という，はっきりとした物理的意味を有しています （2.2節参照）．

=== 表1.3　マグニチュードの解説 ===

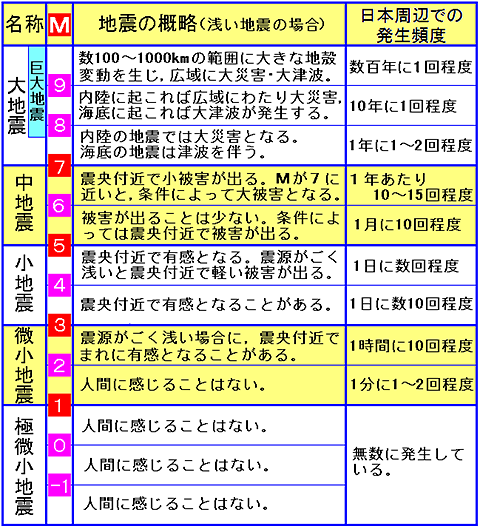
　地震は，その規模の大小によって，表1.3に示すとおり，大地震( M7以上)，中地震(M7未満でM 5以上)，小地震(M5未満でM 3以上)，微小地震(M3未満でM 1以上)，極微小地震( M1未満)と分類されています． 大地震のうちM8程度以上のものは，とくに巨大地震と呼ばれることがあり，1960年チリ地震や1964年アラスカ地震のように世界最大規模のものはM9クラス(モーメント・マグニチュード)まであります．
　これとは逆に，小さな地震の方はM1，M0，M(-1)，M(-2)，．．．と続きます． もともとMは記録された地面の揺れ幅の対数で定義されたことを思い起こせば，これは記録された地動の振幅が10，1，0.1，0.01，．．．と小さくなっていくことを意味しています． 当然，小さな地震になるほど，実際の場面ではその捕捉が困難になります．

=== 表1.4　日本周辺で1997〜2016年の20年間に発生したマグニチュード別の地震回数（気象庁地震カタログによる） ===

　表1.4は，日本周辺（（37.5N，137.5E）を原点として東西 -900〜+900km，南北-950+950kmの範囲）で最近の20年間（1997〜2016年)に発生した地震の回数をマグニチュード別に集計したものです．
中規模以上の地震数は時々大幅に増えていますが，これらは2000年伊豆諸島の群発地震活動や，2003年十勝沖地震，2004年新潟県中越地震，2011年東北地方太平洋沖地震，2016年熊本地震と，それに伴う激しい余震活動によるものです．
なお，小さな地震の数が2000年以降急増しているのは，気象庁の震源決定に防災科研高感度地震観測網(Hi-net)のデータが使用されるようになったためです．
　この20年間を平均すると，我が国でM7以上の地震は年に1〜2個，M6以上の地震は年に15個（月に1個）程度，M5以上の地震は年に110個（月に10個）程度，M4以上の地震は年に1,000個（毎日3個）程度発生しており，一方，M3以上の地震は毎月500個（毎日15個）程度，M2以上の地震は毎日60個程度発生しています． また，観測される全地震数は年に13万個（月に1万個，毎日350個）程度という膨大な数にのぼっています．

=== 図1.5　1990-1999年の10年間に関東・東海地域で発生した深さ100km未満の地震の震源分布（防災科研データによる）．(a)M4以上，(b)M4未満 ===

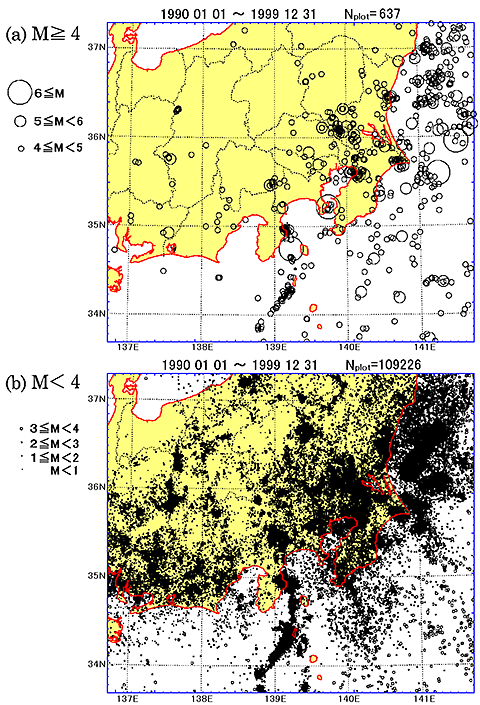
　規模の大きな地震はめったに発生しませんが，中小の地震は数多く発生しています． 図1.5は，1990〜1999年の10年間に関東・東海地域で検知された深さ100km未満の地震を，(a)M4以上，(b)M4未満に分けて，その震源分布を示したものです(防災科学技術研究所の資料による)．

　記号の大きさはMの大小に対応しており，(a)，(b)それぞれの地震数は，637個（平均すると月に5個） および109,226個（平均すると月に900個）となっています． 小さな地震の発生数はいかに多いかということが実感できるでしょう．

=== 図1.6　1949〜1998年の50年間に日本周辺で検知された地震のM別頻度分布（気象庁データによる） ===

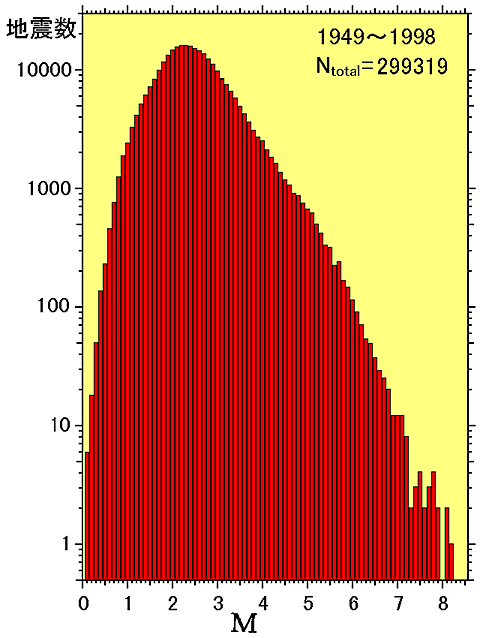
　ところで，日本全域で見た場合，マグニチュード別の地震発生回数はどの程度になっているのでしょうか？ 図1.6は，1949〜1998年の50年間に日本とその周辺で発生した地震の数をMが0.1ごとに集計し，その結果を棒グラフにしたものです(気象庁の資料による)．
　この50年間に発生した地震数は， M8級が3個，M7級が52個，M6級が502個，M5級が3,640個，M4級が14,224個となっています． この数字を50で割って，平均的な年間の地震発生率を求めると，M8級が0.06個/年，M7級が１個/年，M6級が10個/年，M5級が73個/年，M4級が284個/年となります．

　図1.6では，縦軸が対数目盛にとってあり，Mが3から7くらいの範囲では，地震数nがほぼ直線状に減っていく分布となっています． 数式で書くと，この直線部分は
　log( n ) = a - b M
と表わすことができます．この式はグーテンベルグ-リヒター(Gutenberg-Richter)の関係式と呼ばれ，地震統計の基本となっています．
　直線の傾きを表わす係数bは，しばしば「b値」と呼ばれ，大きな地震と小さな地震の発生頻度の比を表わす重要なパラメータです． b値は通常0.9〜1であり，これは，Mが1だけ小さくなると発生する地震数は8〜10倍に増え，Mが2小さくなると地震数は64〜100倍に増大することを意味しています．

　なお，図1.6で，M3くらいより小さな地震の数がこの直線から外れて少なくなっていくのは，地震観測網の検知能力の限界によって，あまりに小さな地震は捕捉できなくなるためです． 逆に，このような直線関係からのずれを見ることにより，観測網の地震検知能力を評価することができます．
　図1.6をくわしく見るとM５くらいのところにも折れ曲がりが見られ，50年間の検知能力は一様ではなかったことが伺えます． また，M8付近の地震数もこの直線から外れますが，これは，そもそも地震の発生回数が低くサンプル数が少ないためです．