図2.2で示したように， 地震が発生すると，地下ではまずある1点で岩盤の食い違いが生じ，それが周囲に伝播して， ある広がりをもった断層面が形成されます． 岩盤が食い違いを起こすと，その動きは振動となって周囲の媒質に伝わっていき， やがて地表に届くことになりますが，これを「地震波」と呼びます．
　地震波の放出は，断層面の形成が完了するまで，破壊の伝播につれ連続的に行われますが， これは，救急車がサイレンを鳴らしながら走っていく様子に似ています． 救急車の走るスピードが破壊速度，サイレンから出る音波が地震波に相当します． 地表に届く最初の地震波は，破壊の開始点，すなわち「震源」から発せられたものですが， この位置がどこであるかを推定する作業が「震源決定」です．

　一方，その地震によって地中に生じた断層面が空間的にどのような向きであり， 断層面上ではどのような方向に岩盤の食い違いが生じたのかを明らかにする作業が「発震機構解決定」です． 発震機構を求めることによって，震源付近ではどのような力が加わり， どのような断層運動が生じたかを知ることができます．

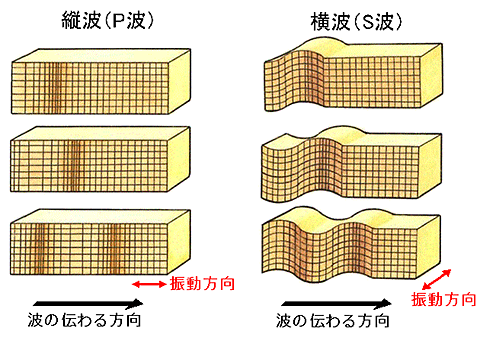
　地震がどこで起きたか（正確には，地震による破壊の開始点がどこであったのか）を知るためには， 観測される地震波が地球の中をどのように伝わってきたかを知る必要があります． 地震波が地球内部を通過する伝わり方には次の2通りがあります． ひとつは媒質（波を伝える物質）の振動方向が波の進む方向と平行な「縦波」であり， もうひとつは媒質の振動方向が波の進む方向に垂直な「横波」です （図3.1）．

=== 図3.1　地震波の伝わり方（科学技術庁パンフ「大地震のあと，余震はどうなるか」より） ===

　縦波は，媒質が局所的に体積を膨張させたり収縮させたりする状態を次々と伝えるもので， 「粗密波」とも呼ばれます．これは音波が伝わっていくのと同じ方式です． 一方，横波は，媒質が局所的に横ずれする状態が次々と伝わっていくもので，「捩れ波」とも呼ばれます． 流体はこのような動きを隣りに伝える能力がないため，流体中では横波は存在しません．

　地震波の伝わる速度は縦波の方が速く，横波の伝播速度は縦波の60〜70％程度であることが普通です． 地震波を観測していると，縦波が1番目(Primary)にやってきて，横波は2番目(Secondary)に到着するため， 両者は通常「P波」，「S波」と呼ばれています． 地表付近ではP波速度が5km/sec前後，S波速度は3km/sec前後となっています．

　震源決定の原理を説明するため，まず簡単のために地中のP波速度Vp， およびS波速度Vsがともに一定な媒質（均質媒質）を考えましょう． 震源から観測点までの直距離（震源距離）をrとすれば， P波およびS波が震源を出てから観測点に到達するまでの時間（走時）はそれぞれ r/Vp，r/Vs なので， 観測点においてP波が到着してからS波が遅れてやってくるまでの時間 t_S-P（これをS-P時間と呼ぶ）は， t _S-P=r/Vs - r/Vp=(1/Vs- 1/Vp) r となります． (1/Vs- 1/Vp)は定数ですから，S-P時間は震源距離 r に比例することになります．

=== 図3.2　S-P時間と震源距離との関係（科学技術庁パンフ「地震の発生メカニズムを探る」より） ===

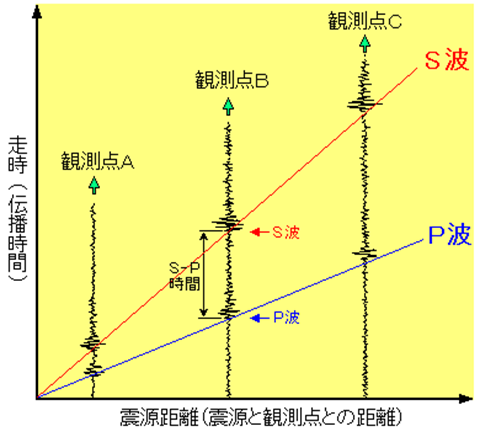
　図3.2は，この様子を図にしたものです． 縦軸は時間，横軸は震源からの距離となっており，各地での地震波形が示されています． P波は早く到達し，S波は遅れてやってきますが，その遅れ具合は距離が遠くなるほど大きくなります． これは，始発駅を同時に出発した急行列車と鈍行列車の到着時刻が段々ずれていくのと同じことです．

　したがって，S-P時間を計れば，観測地点から震源までの距離を r =k t _S-P （ここで，k =1/(1/Vs- 1/Vp)）によって知ることができます． この係数 k は，日本の地震学創世紀の頃の地震学者の一人である大森房吉の名にちなんで「大森定数」と呼ばれています． たとえばVp=5km/sec，Vs=3km/secの場合には k =7.5 km/secとなるので，S-P時間の秒数に7ないし8を掛ければ， 震源までのおおよその距離(km)を見積もることができます．

　このようにして，3つの観測点A，B，CでS-P時間が測定されると， 各観測点から震源までの距離 r_A，r_B，r_Cが定まるので， あとは各点から半径 r_A，r_B，r_Cの球面の交点として幾何学的に震源位置が決定できます．具体的には，3点 A，B，Cから長さ r_A，r_B，r_Cのひもをぶらさげ， その先端をひとつにまとめた位置が震源ということになります．

=== 図3.3　震源位置の図式解法（力武常次「地球科学ハンドブック」聖文社より） ===

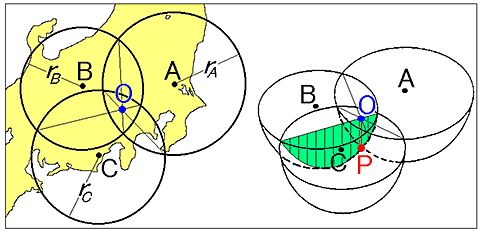
　これを図式で行なうには，まず図3.3に示すように 3点 A，B，Cを中心として半径 r_A，r_B，r_Cの円を描き， その共通弦の交点として震央位置Oを定めます．球面同士の交わる線は円となるので， 共通弦（どれでもよい）を直径とする断面円を描いてOの位置から垂線を立てれば， この垂線と断面円との交点Pが震源位置となり，長さOPが震源の深さを表わすことになります．

　以上は，地球内部を均質であると仮定した，最も簡単な場合の話でした． このとき，震源から出た地震波の波面は図3.4の上段に示すように 同心円状となります．また，波面に垂直で，波の進む方向を表わす「波線」は単純な放射状の直線になります．

=== 図3.4　地震波の伝播(上段：均質媒質の場合，下段：地震波速度が深さ方向に増大する場合) ===

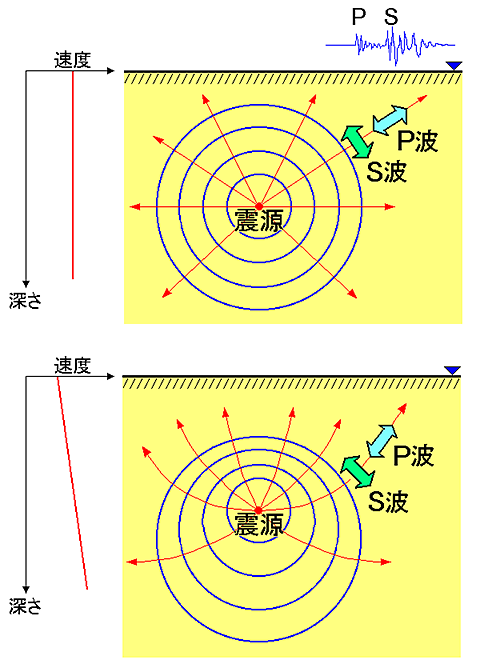
　しかし，現実の地球内部はもっと複雑であり，場所によって地震波速度が異なる不均質状態となっています．とくに地球深部では高圧の状態となっているため，一般に，地震波速度は深くなるほど増大することが知られています．

　図3.4の下段には， 地震波速度が深さ方向に直線的に増大している場合の地震波の伝播状況が示されていますが， 波線はもはや直線ではなく，曲線になります． このような場合，震源を発した地震波が観測点に到達するまでの時間（走時）は， 均質媒質のときのように単純な式で表わすことはできません． しかし，地震波速度の垂直分布が与えられれば，走時は計算することができます．

　実際の震源決定では，震源の深さと震央距離の関数としてP波およびS波の走時を求めるプログラムを 電子計算機の内部に組み込み，地震の発震時と震源の位置を少しづつ変えながら， 観測されたP波およびS波の着震時データと理論的な走時がもっとも良く適合する組合せを探すという作業を行なっています．

　精密な震源決定を行なうためには，地下の詳細な地震波速度構造があらかじめわかっている必要があります． しかし，その地下構造は，震源決定から得られる震源位置と発震時，および観測された着震時に基づいて推定がなされます．
　すなわち両者は”にわとりと卵”のような関係にあるわけですが，様々な工夫をこらすことによって， 両者を逐次精密化していく作業が続けられています．