地震が発生すると，地下ではまずある1点で岩盤の食い違いが生じ，それが周囲に伝播して， ある広がりをもった断層面が形成されます（図2.2）．

=== 図3.5　断層モデル ===
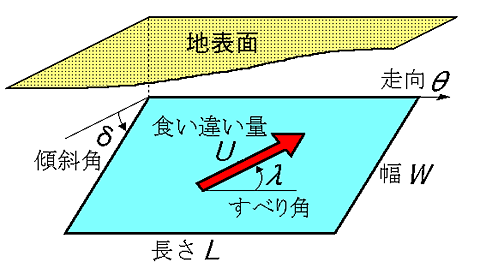　このような断層運動を記述するためには，断層面の位置（緯度，経度，深さ）のほか， 図3.5に示すように， 断層面の大きさ（長さL，幅W ）と向き（走向θ，傾斜角δ）， および断層面上での食い違いの大きさ(U )と向き（すべり角λ）の，計6つのパラメータが必要となります．
　これらのうち，断層面の向きとその面上での食い違い方向を表わす３つのパラメータ(θ,δ,λ)を求める作業が 発震機構解決定です． 断層面の大きさ(L,W )と食い違い量(U )は，余震の分布や地震波形，地殻変動などから，別途推定されます．

=== 図3.6　震源球と押し引き分布．右側は赤道面で切った断面を示す． ===
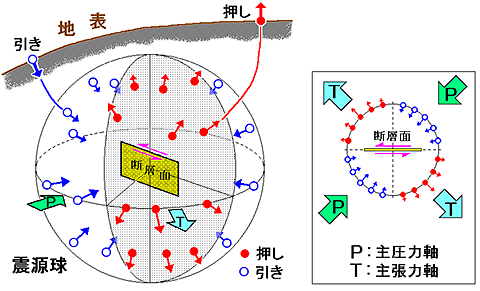　発震機構解を求めるためには，各観測点で記録された地動の初動方向， すなわち最初に地面が上がったか下がったかという情報を用います．
　図3.6で示すように， 震源を取り囲む仮想的な小球面（震源球）を考え，観測された初動極性データを波線に沿って震源球まで戻してやると， 震源球面上に「押し」（初動up）と「引き」（初動down）の分布ができます． 図3.6の右側に示されているように， 断層運動によって周囲の媒質は４象限型に動くことが期待されるため， 直交する2枚の平面（節面）によって震源球面上の押し引き分布を上手に分離することができれば， そのうちの一方が断層面であり，他方の面に直交する向きに食い違いが生じたことになります．

　実際の発震機構解決定では，震源球を平面上に投影して， 押し引き分布をもっとも良く分離するような直交大円の組み合わせを図上でさがし求める方法のほか， 電子計算機の内部で２枚の直交面の組み合わせをしらみつぶしに試して， その中から，観測された押し引き分布をもっとも矛盾なく説明できるものを選ぶ作業を行なったりしています．
　発震機構解の解析では２つの直交する節面が最終結果として得られますが， そのどちらが断層面であるかは特定できません． 断層面の決定については，ある程度大きな地震であれば余震の配列や地表の変形状況等から判断できる場合がありますが， そうでない場合は，地震波形を詳細に調べて推定された破壊伝播方向から判断したり， または，テクトニクス的な考察に基づいて妥当な方を選択するなどの手段がとられます．

　以上に述べた発震機構解の求め方は地震波初動（P波）の押し引き分布に基づいているため， 厳密に言えば，その結果は，地下での破壊が震源で開始された瞬間における断層運動の様子を表わしているにすぎません． 近年，広帯域地震計等を用いた良質の長周期地震記録が得られるようになったため，初動極性のみでなく， 観測された地震波形全体をデータとして用い，理論的に予測される波形と比較することによって， 総体としての断層運動を調べることが盛んに行なわれるようになってきました．
　この場合，最終的な断層面の大きさに比べて十分遠方の場所に置かれた地震計の記録を使用し， 断層面全体をその重心で代表されるひとつの点とみなして解析を行うことが普通で， その結果はCMT(Centroid Moment Tensor)解と呼ばれます． このような解析では，断層面や食い違いの向きだけではなく，地震波形の振幅データを用いて， 断層運動の強さ（地震モーメント）も同時に推定することができ， 断層面の面積と食い違い量との積(LWU )に関する情報を得ることができます．

=== 図3.7　発震機構解の表示法 ===
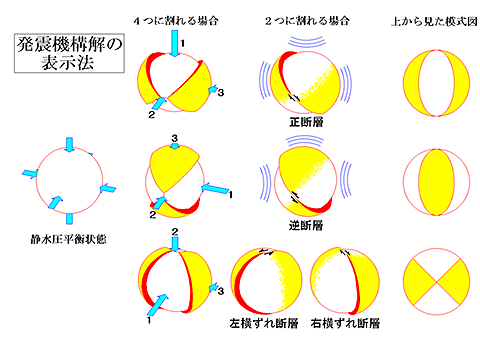　ところで，断層運動は空間における３次元的な動きであるため，これを図式で表現することはなかなか困難です． 図3.7では， 発震機構解を表わすために通常用いられている表現法とその意味を図解しています．
　同図左端は震源球が静水圧平衡の状態にある場合で，あらゆる方向に同じ圧力が働いています． しかし，この平衡状態が破れて力が不均衡になると，やがて様々なモードの破壊が生じ， 震源球は４つまたは２つに割れることになります． 慣習上，周囲から働く圧力が最大である方向を主圧力軸またはP軸， 最小である方向を主張力軸またはT軸と呼びますが，P軸，T軸の方位とこれにより生じる断層運動とは， 図3.6の右側に描かれたような関係になっていて， 断層面とP軸またはT軸は45度の角度をなします．
　なお，図3.6では， T軸が震源から外の方向に向かう引っ張り力のように描かれていますが， これはあくまで全体としてかかる平均的な圧力を基準とした場合の相対的な表現であって， 現実に働いている力は，図3.7に見られるとおり， すべて圧縮力の状態です．

　さて，図3.7には， このP軸とT軸の組み合わせの違いによって，３通りの破壊様式が示されています． 上段はP軸が鉛直方向，T軸が水平方向にある場合で， このときは断層面の上盤側がずり落ちる「正断層」と呼ばれる割れ方を生じます． ４つに割れる場合は，両節面とも正断層運動を示すことになります． 次に中段はT軸が鉛直方向，P軸が水平方向にある場合で， このときは上盤側がのし上がる「逆断層」という割れ方を生じます． これも，４つに割れる場合の両節面はともに逆断層運動を示します．
　下段はP軸，T軸がともに水平面内にある場合で， このときは垂直な断層面を境として両側の岩盤が横にずれるタイプの断層を生じます． 断層面に向かって立った時，相手側のブロックが右に動く場合を「右横ずれ断層」， 左に動く場合を「左横ずれ断層」と呼びます． 震源球が４つに割れる場合は，片方が右横ずれ，他方が左横ずれとなります．

　以上のすべての場合について，黄色で示した四半球部分（T軸部分）は押しが弱いために外側へ押し出され， 一方，白く描かれた四半球部分（P軸部分）は強い押しのために内側へ引きずり込まれる向きの動きが生じます． このような震源での動きは隣りから隣りへと伝播し， 地表の地震観測点に対してそれぞれ「押し」と「引き」の初動を与えることになるわけです．
　このような断層運動の状況を模式的に表わすため， 通常，図3.7の右端にあるような表現方式がとられており， これを発震機構解図と呼びます． これは，震源球を水平面で切断して，その下半球を上からのぞいた図になっています． 黄色の部分が押し（T軸）の領域，白い部分が引き（P軸）の領域に相当し， ２つある両者の境界（節面）のいずれかが断層面に対応しています．

=== 図3.8　実際の発震機構解の例 ===
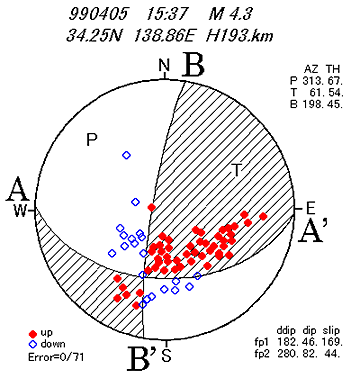　現実の断層運動では，図3.7のように P軸やT軸がちょうど鉛直や水平方向にあるとは限らず，したがって，震源球の割れ方も同図を空間的に回転させたような状態で生じることが一般的です． このため，発震機構解図も，図3.7に示された基本的パターンが組み合わされたような中間的なものとなります．

　たとえば，図3.8に示す実際例では， 節面AA'をとると，南へ傾く面上の右横ずれ断層に若干の逆断層成分が含まれていることになり， 節面BB'をとれば，西へほとんど垂直に傾く面上の逆断層に左横ずれ成分が含まれていることになります．
　このような図を見る場合，卵や果物を詰めるのに使われる直交の仕切り板がお椀の中にセットされている状態を 想像すれば，多少とも空間的なイメージをつかめるかもしれません．